象歩将棋

Webと将棋で何か具体的なもの作って行こうとしてます。

454  shu  2008/04/16 22:43 id: 3BVR6NRi4pQ  prob: 0.4%

性能だけ考えてます(爆
申し訳無い。(>>451, >>452) の記事は人を惑わすだけだと思いました;;
実際、今私の脳内が混乱してます(笑

[モデル-1]
局面集合を辞書 S{キー値、局面情報} で持ち、局面探索機能は一個のオブジェクトが持ちます。
XOR 演算を利用すると、ある局面 Si から次の局面に遷移するには乱数 Ri を用いて、
Si+1 = Si ^ Ri で済みます。乱数 Ri はあらかじめ計算して置くことができるので、
うまく値を設定すれば S1,2,....n が広く分散し、辞書のキーに使えるのではないかと云うこと。
つまり、Ri の選択と Si ^ Ri 演算だけで高速にノード間を渡り歩くことができると云うことらしい。

この場合、たとえばキーを 64bit 局面情報を 64bit とすると、一億局面を収めるには、
(64 + 64) * 100,000,000 = 12,800,000,000 = 12.8Gbit = 1.6GB 必要になる。
そして同一局面であることを判断するには局面情報の比較が必要となる。

[モデル-2]
ひょっとしてキーで局面も表現できるのではないかと考えました。
そうすれば局面集合は S[キー値] の配列で表現できます。

例えば玉を K11→K22 と移動するとき、K11→K12→K22 と K11→K22 を考えてみます。
ここで R(11,22) = R(11,12) ^ R(12,22) とすれば
K22 = K11 ^ R(11,12) ^ R(12,22) と K22 = K11 ^ R(11,22) は同じことです。
てことで乱数をうまく設定できるのならばキー値は局面を表すことになり、
1) 配列要素に局面情報は入れずノードの状態のみ2bitで表すとすれば一億局面25MBですむ。
2) 同一局面であることを判断するにはキー値を直接比較すれば良い。
なんて都合の良いことを妄想していました。てことで、あくまで妄想です。。。(孟宗竹は美味い^^)

453  pon  2008/04/16 12:52 id: 480oHczCgMM  prob: 2.7%

同一局面の話し（なら）：性能無視のとき（勘違いしてるかも^^;）
/**　局面PGm == 局面PGn ?
 *  40 * 40 = Max1600 loop
 */
Iterator it = PGm.getPieceList().iterator();
for(it.hasNext()) {
    if(!it.next().isEqual(PGn)) {
       break;    //等しくない
   }
}
// Piece.isEqual()
protected boolean isEqual(PG target) {
//TO DO 駒の比較項目
//   手番、種類、成り有無、位置(x,y：駒台時は0,0)

}

452  shu  2008/04/15 23:01 id: 3BVR6NRi4pQ  prob: 31.9%

ハッシュキーは局面を表さないといけない。
たとえば無双一番を11手探索した時点で、未解決局面が 1,747,982 個、
そのうち重複してるのが 949,725 局面ありました。
さらに深い探索をすると約半分のノードの探索は無駄ということになる。
探索局面の重複をすぐに判別できないなら意味が無い。

ハッシュキーを生成するためには、
1) ある駒を x あるいは y 方向に移動する場合のランダムな自然数 R(x), R(y) を決める。
2) x,y 同時に移動する場合は R(x,y) = R(x) ^ R(y) とする。
3) 上記乱数を(成)駒の種類と成りについて各々求める。
4) 駒を獲得する場合、XOR演算工程を1ステップ追加。
5) 駒を打つ場合も別。
かなり大雑把ですが。

451  shu  2008/04/14 23:18 id: 3BVR6NRi4pQ  prob: 5.0%

ツリー探索はやはり Zobrist 利用?
ゲーム木では定番のセオリらしい。
http://fragrieu.free.fr/zobrist.pdf
http://mm.cs.uec.ac.jp/doc/ipsj2002.pdf

大量の局面を配置するのに便利なのだろう。
前後の局面アドレスがすぐに求められるので、高速ツリー探索に使えるのだと思う。
そう言ってもまだ理解してるわけではありません。

ハッシュキーは局面を表すものでは無いので(たぶん)、
同一局面のヒットはまた別に考えないといけないのかな。
大量のメモリを消費するのが気になる。

$ python
>>> s0=0
>>> n1=1
>>> n2=2
>>> n3=4
>>> s3 = s0^n1^n2^n3
>>> s3
7
>>> n3^s3
3
>>> n2^n3^s3
1
>>> n1^n2^n3^s3
0

450  shu  2008/04/10 21:03 id: 3BVR6NRi4pQ  prob: 1.4%

作戦を継続するには一筆書きでは困難。
ノードをばらし評価関数導入することが必要になります。
処理速度は一億手/100秒くらい出てるので計算する手数を減らす戦略。

ひとつのノード {手、評価値、上位へのポインタ、局面コンテキスト} で 24byte 必要。
とすると直線的には一億手で約 2GB くらいのメモリが必要ですが。Φ

449  shu  2008/04/08 21:47 id: 3BVR6NRi4pQ  prob: 0.9%

プロローグ
詰将棋も平手将棋と同じく無限性を考慮すれば、
詰む確率、詰まない確率の評価が重要なのでしょう。

今回はビット演算を利用して実装してみましたけれど、
ロジックは C++ ソースコードの中に直書きされて居るので、発展性がありません。
とはいえ内部処理は集合演算そのものなので汎用化する道はあります。
たとえば必要な要素をプリミティブなオブジェクトなり演算子として実装し直すとか。

サンプルとして、詰みが成立する局面のことを考えてみると、
--
1) 攻め駒が一枚だけで詰みとなる場合は、
  必要条件: K ⊆ *Br
    (玉 K には攻め方の駒 Br が利いてること)
  十分条件: ?K == φ AND (K...Br] ⊄ Σ*Wi
    (玉 K は移動できない、かつ攻め方の駒 Br までの範囲に玉方の駒が利かないこと)

2) 攻め駒が二枚以上で詰みとなる場合は (1) に加え
  必要条件: K ⊆ *Bx AND Bx ⊆ *By
    (玉 K には攻め方の駒 Bx が利いてる、かつ Bx に味方の駒 By が利いていること)
  十分条件: ?K == φ AND (K...Bx] ⊄ Σ*Wi (ただし Wi は K を含まない)
    (玉 K は移動できない、かつ攻め方の駒 Bx までの範囲に玉以外の玉方の駒が利かないこと)

# K は位置、*K は利き位置の集合、?K は移動可能位置の集合を意味します。
# 正確でも厳密な記述でもありませんので、余計なことで悩まないでください。(空き王手ははぶいてるし)

448  shu  2008/04/07 21:42 id: 3BVR6NRi4pQ  prob: 3.0%

速度の比較
参考までに詰パラ二月の懸賞問題で実行してみた。
Pentium4 2.8EG:  5.30 秒
Athlon64x2 3800: 1.05 秒
Athlon64 3700+:  0.95 秒
(1,095,025 局面)
残念ながら、現在のWEB鯖 (Pen3 800EB) に乗せるのは無理みたい。
ならば当面 Athlon64 3700+ を将棋鯖に改造するしかないかの。

447  shu  2008/04/06 22:32 id: 3BVR6NRi4pQ  prob: 0.7%

たどり着いてやはり麓
先手は"詰むや"の評価が必要。
後手は"詰まざるや"の評価が必要。
今はほとんど使って無いメモリの有効利用が扉を開く鍵となるのであろうか?
たとえば、先後の候補手が 1/3 の範囲に収まるだけで極めて効率が良くなるのは想像できる。

http://www.geocities.jp/k_7ro/
http://www005.upp.so-net.ne.jp/tsumepara/contents/4appre/mc/...
その過程でミクロコスモスが解ければ嬉しいとは思うけど、
本当の敵はポン能寺なので、うまく立回らないといけない。

446  shu  2008/04/06 21:28 id: 3BVR6NRi4pQ  prob: 0.1%

二歩と打歩詰ルールを追加。
千日手や無駄な合駒は探索中に考えれば良いことだし、
そもそも正解手順には現れない(ように設定できる)。
また持将棋ルールは詰将棋に関係ない。
と云うことで必要なルールはすべて実装できたみたい。
ソースは C++ で 3,840 行。

445  shu  2008/04/05 21:36 id: 3BVR6NRi4pQ  prob: 0.7%

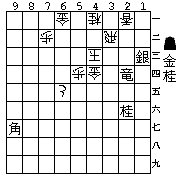
無双第一番が解けない。
カンニングして正解手順を６手進めたところから探索。

▲３三竜 △５二玉 (正解は同玉) ▲５三金 △同桂 ▲同角成 △４一玉
▲３二竜 △同玉 ▲３一飛 △２三玉 ▲２一飛 △３二玉
▲２四桂 △２一玉 ▲３三桂 △１一玉 ▲１二香までの１７手詰め (+６手)。

100,147,641局面 / 110秒 (消費メモリは約1MB)

やはり手の優先順位の影響が大きいようです。たとえば攻め方は成る手を優先するとかはあたりまえですね;;
案の定、喜びの次の日には厚い壁が立ちはだかってましたが、これでやっと扉をさがす旅に出られます。

実装として一億手余りまでは馬鹿読みながら可能なことは確認できました (いや驚いたね;;)。
数年後には一秒で一億と四手を読むことが現実になるのだろうなぁー